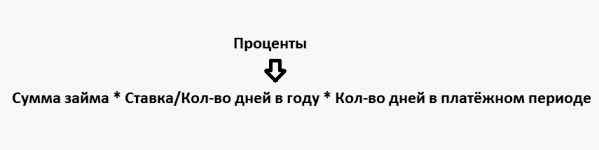
Точное число дней ссуды

Простые и сложные проценты

Наращение может осуществляться по схеме простых и слож­ных процентов.

Формула наращения простых процентов (simple interest). Нара­щение простых процентов означает, что инвестируемая сумма ежегодно возрастает на величину PV • r. В этом случае размер инвестированного капитала через n лет можно определить по формуле:

Формула наращения сложных процентов (compound interest). Наращение по схеме сложных процентов означает, что очеред­ной годовой доход исчисляется не с исходной величины инвести­рованного капитала, а с общей суммы, включающей также ранее начисленные и не востребованные инвестором проценты. В этом случае размер инвестированного капитала через n лет можно оп­ределить по формуле:

При одном и том же значении процентной ставки:

1) темпы наращения сложных процентов выше темпов нара­щения простых, если период наращения превышает стандартный интервал начисления дохода

2) темпы наращения сложных процентов меньше темпов на­ращения простых, если период наращения меньше стандартного интервала начисления дохода.

Области применения простых и сложных процентов. Простые и сложные проценты могут применяться как в отдельных опера­циях, так и одновременно. Области применения простых и слож­ных процентов можно разделить на три группы:

1) операции с применением простых процентов

2) операции с применением сложных процентов

3) операции с одновременным применением простых и сложных процентов.

1. Областью применения простых процентов чаще всего явля­ются краткосрочные операции (со сроком до одного года) с од­нократным начислением процентов (краткосрочные ссуды, век­сельные кредиты) и реже — долгосрочные операции.

При краткосрочных операциях используется так называемая промежуточная процентная ставка, под которой понимается го­довая процентная ставка, приведенная к сроку вложения денеж­ных средств. Математически промежуточная процентная ставка равна доле годовой процентной ставки. Формула наращения простых процентов с использованием промежуточной процент­ной ставки имеет следующий вид:

FV = PV (1 + t • r / Т),

t — срок вложения денежных средств (при этом день вложения и день изъятия денежных средств принимаются за один день) Т — расчетное количество дней в году.

При долгосрочных операциях начисление простых процентов рассчитывается по формуле:

где n — срок вложения денежных средств (в годах).

2. Областью применения сложных процентов являются дол­госрочные операции ( со сроком, превышающим год), в том числе предполагающие внутригодовое начисление процентов.

В первом случае применяется обычная формула начисления сложных процентов:

Во втором случае применяется формула начисления сложных процентов с учетом внутригодового начисления. Под внутригодовым начислением процентов понимается выплата процентного дохода более одного раза в год. В зависимости от количества вы­плат дохода в год (m) внутригодовое начисление может быть:

1) полугодовым (m = 2)

2) поквартальным (m = 4)

3) ежемесячным (m = 12)

4) ежедневным (m = 365 или 366)

5) непрерывным (m -» ?).

Формула наращения при полугодовом, поквартальном, еже­месячном и ежедневном начислении сложных процентов имеет следующий вид:

FV = PV (1 + r / m) nm ,

где PV — исходная сумма

г — годовая процентная ставка

n — количество лет

m — количество внутригодовых начислений

FV — наращенная сумма.

Процентный доход при непрерывном начислении процентов рассчитывается по следующей формуле:

где: e = 2, 718281 — трансцендентное число (число Эйлера)

е. n — множитель наращения, который используется как при целом, так и дробном значении n

— специальное обозначение процентной ставки при непрерыв­ном начислении процентов (непрерывная процентная ставка, «сила роста»)

n — количество лет.

При одинаковой величине исходной суммы, одинаковом сро­ке вложения денежных средств и значении процентной ставки возвращаемая сумма оказывается больше в случае использования формулы внутригодовых начислений, чем в случае использова­ния обычной формулы начисления сложных процентов:

FV = PV (1 + r / m) nm > FV = PV (1 + r) n .

Если доход, полученный при использовании внутригодовых начислений, выразить в процентах, то полученная процентная ставка окажется выше той, которая использовалась при обычном начислении сложных процентов.

Таким образом, первоначально заявленная годовая процент­ная ставка для начисления сложных процентов, называемая но­минальной, не отражает реальной эффективности сделки. Про­центная ставка, отражающая фактически полученный доход, на­зывается эффективной. Классификацию процентных ставок при внутригодовом начислении сложных процентов наглядно иллю­стрирует рисунок.

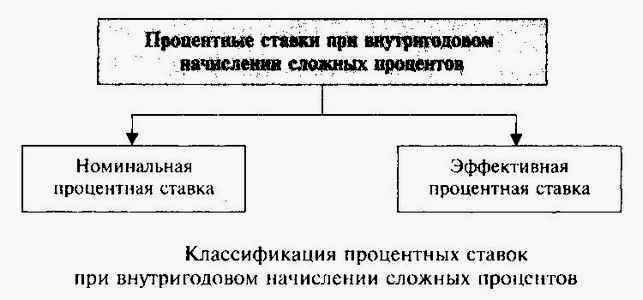
Номинальная процентная ставка задается изначально. Для каждой номинальной процентной ставки и на ее основании мож­но рассчитать эффективную процентную ставку (r_е ).

Из формулы наращения сложных процентов можно получить формулу эффективной процентной ставки:

Приведем формулу наращения сложных процентов с внутригодовыми начислениями, при которых каждый год начисляется r / m процента:

FV = PV (1 + r / m) nm .

Тогда эффективная процентная ставка находится по формуле:

где r_е — эффективная процентная ставка r — номинальная процентная ставка m — количество внутригодовых выплат.

Величина эффективной процентной ставки зависит от коли­чества внутригодовых начислений (m):

1) при m = 1 номинальная и эффективная процентные ставки равны

2) чем больше количество внутригодовых начислений (значение m), тем больше эффективная процентная ставка.

Областью одновременного применения простых и сложных процентов являются долгосрочные операции, срок которых со­ставляет дробное количество лет. При этом начисление процентов возможно двумя способами:

1) начисление сложных процентов с дробным числом лет

2) начисление процентов по смешанной схеме.

В первом случае для расчетов применяется формула сложных процентов, в которой присутствует возведение в дробную сте­пень:

FV = PV (1 + r) n + f ,

где f — дробная часть срока вложения денежных средств.

Во втором случае для расчетов применяется так называемая смешанная схема, которая включает формулу начисления слож­ных процентов с целым числом лет и формулу начисления про­стых процентов для краткосрочных операций:

FV = PV (1 + r) n • (1 + f • r),

FV = PV (1 + r) n • (1 + t • r / Т).

2.5. Способы начисления процентов

Существуют два способа определения и начисления процентов.

Декурсивный способ начисления процентов: проценты начисляются в конце каждого интервала начисления. Их величина определяется, исходя из величины начального капитала .

Антисипативный способ начисления процентов (предварительный). проценты начисляются в начале каждого интервала начисления . Сумма процентных денег определяется, исходя из наращенной суммы .

2.6. Основные схемы начисления процентов

А. В зависимости от базы начисления процентов . известны две основные схемы дискретного начисления процентов: схема простых и схема сложных процентов.

Схема простых процентов (simpleinterest ) предполагает постоянную базу для начисления процентов - одну и ту же первоначальнуюденежную сумму в течение всего периода начисления.

Инвестированный капитал ежегодно увеличивается на одну и ту же величину.

Схема сложных процентов (compoundinterest ) предполагает переменную базу для начисления процентов. Очередной годовой доход исчисляется не с исходной величины инвестированного капитала (как для простых процентов), а с общей суммы, включающей также и ранее начисленные за предыдущие интервалы и не востребованные инвестором проценты.

В этом случае происходит капитализация процентов, т.е. присоединение начисленных процентов к их базе. Следовательно, база, с которой начисляются проценты, все время возрастает. Сложные проценты иначе называют "проценты на проценты ".

Б. Процентные ставки в зависимости от постоянства значения в течение действия контракта могут быть фиксированными и плавающими .

В. В зависимости от постоянства интервала времени начисления процентов (год, полугодие, квартал и т.п.) проценты могут быть дискретными и непрерывными ( за бесконечно малые промежутки времени).

3. НАЧИСЛЕНИЕ ПРОСТЫХ ГОДОВЫХ ПРОЦЕНТОВ

- величина первоначальной денежной суммы - долга, инвестиции,

- наращенная сумма в конце срока,

% - простая годовая ставка ссудного процента (ставка наращения),

- проценты за весь срок ссуды (ден. ед.),

- продолжительность периода начисления в годах (срок ссуды),

- число месяцев ссуды,

- число дней ссуды,

- сумма процентных денег, выплачиваемых за год,

- временнáя база для расчета процентов.

Схема простых процентов :

1) начисление процентов в конце интервала начисления (декурсивный способ начисления процентов)

2) простые процентные ставки применяются к одной и той же первоначальной денежной сумме в течение всего периода начисления, поэтому база для начисления процентов постоянная

3) простые ссудные проценты применяются в краткосрочных финансовых операциях (до года).

По схеме простых процентов за каждый год начисляется одинаковая сумма процентных денег .

В конце первого года наращенная сумма равна

в конце второго года –

в конце-ого года сумма составит

Таким образом, приращение капитала ( проценты за весь срок ссуды лет) составляют

и, как видно, пропорционально сроку ссудыи ставке процента .

Наращенная сумма к концу срока составит

Капитализация процентов выражается формулой

Процентная ставка (в процентах) есть отношение суммы годовых процентных денег к первоначальной сумме .

Заметим, что последовательность наращенных сумм . . . образует арифметическую прогрессию с первым членом и разностью .

_{Множитель наращения простых процентов равен отношению наращенной суммы к первоначальной сумме:}

Он показывает, во сколько раз наращенная сумма больше первоначальной суммы . Другими словами, величина характеризует будущую стоимость одной денежной единицы через лет при ставке процента .

Рис. 1 - График функции наращенной суммы по простым процентам

Пример 4. Ссуда в размере рублей выдана на три года по простой ставке процентов годовых.

Найти сумму процентных денег, выплачиваемых за каждый год.

Записать последовательность сумм, начисленных к концу первого, второго, третьего года.

Найти наращенную сумму за три года.

Каковы проценты за весь срок ссуды?

Найти множитель наращения за три года.

1. За каждый год выплачивается сумма процентных денег

2. В конце первого года наращенная сумма будет равна

в конце второго года –

в конце третьего года - сумма

3. Величину наращенной суммы за три года вычислим по формуле (2):

4. Проценты за весь срок ссуды найдем по формуле (1):

5. Множитель наращения по простым процентам равен

Он показывает, во сколько раз увеличилась первоначальная сумма долга 1000 руб. к концу срока ссуды.

Наращение простыми процентами ежегодно по ставкегодовых дает тот же результат, что и наращение простыми процентами по ставкеза период длительностью(лет).

4. РАСЧЕТ ПРОСТЫХ ПРОЦЕНТОВ ДЛЯ КРАТКОСРОЧНЫХ ССУД

Если банк начисляет в год. то за один день - (число дней в году или ). Тогда за дней ссуды наращенная сумма составит

Определяя продолжительность финансовой операции в днях, принято день выдачи и день погашения суды считать за один день. Для определения в таблице порядковых номеров дней в году (Приложение, Таблица 1) из порядкового номера дня окончания займа вычитается номер первого дня.

На практике используется три способа подсчета . При этом употребляются термины:

Точный процент - точное число дней в году (или 366) дней

Обыкновенный процент – приближенное число дней в году дней

Точное число дней для начисления процентов (количество дней минус 1, так как первый и последний день считаются за один день)

Приближенное число дней для начисления процентов (считается, что в каждом месяце по 30 дней, затем вычитается 1 день).

1 способ. Точный процент с точным числом дней ссуды (США, Великобритания). За временнýю базу берется точное число дней в году ( или ) и точноечисло дней ссуды .

2 способ. Обыкновенный процент с точным числом дней ссуды (Франция, Бельгия). Временнáя база равна приближенному числу дней в году дней, - точномучислу дней ссуды.

3 способ. Обыкновенный процент с приближенным числом дней ссуды - коммерческий процент (Германия, Дания, Швеция). Временнáя база дней, равно приближенному числу дней ссуды (при допущении, что продолжительность любого месяца равна 30 дней.

Источники:
finance-place.ru, works.doklad.ru

Следующие:

• Взять деньги в долг нижний новгород
• Деньги долг в день обращения спб